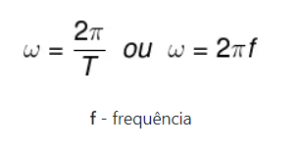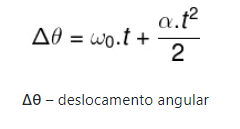Definição
Movimento circular é aquele movimento de rotação de um corpo em torno de um eixo ao longo de uma trajetória circular de raio constante. Se a velocidade de rotação for constante, o movimento é uniforme (MCU). Se a velocidade sofrer variações ao longo do tempo, o movimento é variado (MCUV).
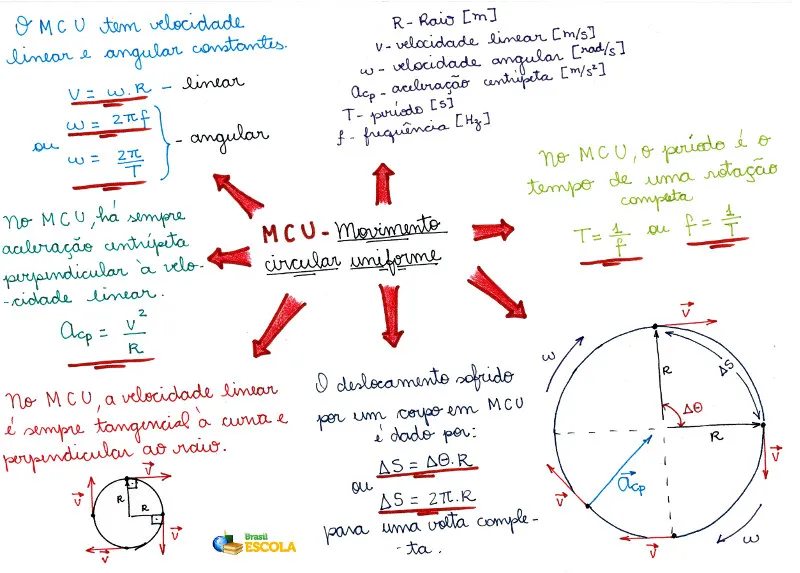
Movimento circular uniforme (MCU)
Como dito há pouco, a velocidade tangencial com o qual o móvel se desloca permanece constante, podendo ser escrita como a divisão entre o deslocamento (ΔS) e o intervalo de tempo do movimento (Δt):
O deslocamento (ΔS) é dado pelo comprimento da circunferência de raio R e é calculado por meio da expressão:
O tempo necessário que o móvel leva para completar uma volta em torno de seu eixo de rotação é chamado de período (T). Portanto, a fórmula da velocidade mostrada acima pode ser reescrita dessa forma:
Baixe o resumo com todas as fórmulas aqui!
Velocidade angular (ω)
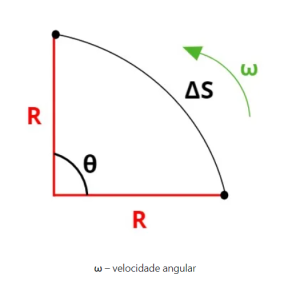
É a variação do ângulo θ formado entre o raio e seus eixos horizontal e vertical, como mostra a seguinte figura:
O valor da velocidade angular média é calculado por meio do deslocamento angular de uma volta completa (2π em radianos) dividido pelo período (T) dessa volta. A fórmula do lado direito é uma segunda forma de calcular a velocidade angular média, uma vez que o período (T) e a frequência (f) de rotação são grandezas inversas. Quanto à unidade de medida da velocidade angular, é utilizado radianos por segundo (rad/s).
Caso você não saiba o período, mas saiba a frequência de rotação, podemos usar a seguinte fórmula:
A unidade de frequência no SI é o hertz (Hz). Outra unidade usada para frequência é o rpm (rotações por minuto). Para convertermos essas unidades, basta lembrarmos que 1 Hz = 60 rpm.
Agora que você sabe calcular a velocidade angular média, você consegue também calcular a velocidade escalar do móvel por meio de outra fórmula:
Movimento circular uniformemente variado (MCUV)
O MCUV ocorre quando a velocidade angular do móvel sofre variações de forma constante com o tempo. Isso quer dizer que a rotação ocorre na presença de uma aceleração angular.
Velocidade angular final
Aceleração angular (α)
Representada pela letra grega alpha (α), a aceleração angular determina a variação da velocidade angular no intervalo de tempo da trajetória.
Onde,
α: aceleração angular média (rad/s2)
ω: velocidade angular média (rad/s)
Δt: intervalo de tempo da trajetória (s)
Deslocamento angular
É a medida de variação do ângulo θ, em radianos, para uma dada velocidade angular inicial (ω0) e para uma determinada aceleração angular (α).
Confira outras coisas que podem te interessar:
Reprodução humana: como acontece?
Classificação Internacional de Doenças. Conheça a CID
Referência da capa: https://brasilescola.uol.com.br/fisica/movimento-circular.htm#Mapa+Mental%3A+Movimento+Cicular+Uniforme